Photonic Quantum Technologies
| Staff members: Esteban Gomez Lopez | |
|
Fundings through: |
|
|
|
Quantenkommunikation Q.Link.X |
1. Quantum Dots as Single Photon Sources
Semiconductor quantum dots are widely investigated as single photon sources for quantum information networks. These so called “artificial atoms” may be used as quantum interfaces between stationary and flying qubits.
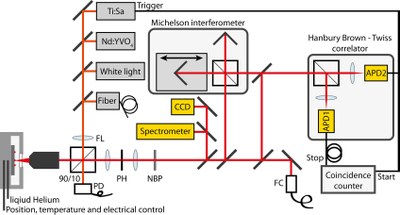
We investigate the optical properties of quantum dot samples in a Helium liquid-flow cryostat. The samples are fully characterized in a confocal high NA microscope setup using different excitation schemes to determine the photon statistics, coherence time of the emitted photons, and the lifetime of different excitonic states in the quantum dot (Fig. 1) [1].
Figure 1: Implemented characterization setup for single photon emission from semiconductor quantum dots. Non-resonant cw and pulsed as well as resonant cw excitation sources are available. A Michelson interferometer and a Hanbury Brown - Twiss correlator are used to determine the amplitude and intensity correlation functions, g(1)(t) and g(2)(t), respectively.
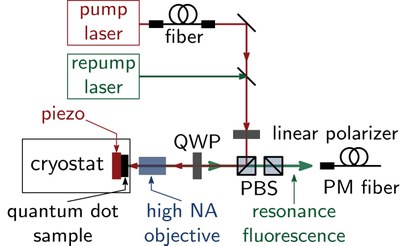
Different tuning mechanisms such as DC or AC electrical fields or strain in the semiconductor lattice are investigated to prepare the stabilization of single quantum dots to the atomic Cesium D1 transition. Resonant photon scattering at the two-level system of a quantum dot exciton allows us to accurately set the quantum dot emission to one of the hyperfine-split Cesium D1 transitions (Fig. 2).
 |
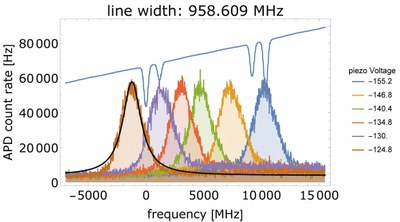 |
Figure 2: Left: Detailed scheme of the resonant excitation. Right: A quantum dot emission line (colored spectra) is tuned by using a piezoelectric material to induce strain into the semiconductor lattice. Such a sample can be used to lock the quantum dot single photon emission to the atomic standard of the Cesium D1 transition. The thin blue line is the measured absorption spectrum of the hyperfine-split states that are used in atomic Cesium clocks.
[1] M. Benyoucef, V. Zuerbig, J. P. Reithmaier, T. Kroh, A. W. Schell, T. Aichele, and O. Benson; “Single-photon emission from single InGaAs/GaAs quantum dots grown by droplet epitaxy at high substrate temperature”; Nanoscale. Res. Lett. 7, 493 (2012)
Contact: Esteban Gomez Lopez
2. Quantum Memories in Hot Alkali Vapors
The implementation of a scalable quantum network nowadays is greatly limited by the intrinsic losses in the channels used to transfer the qubits [1]. To overcome these losses quantum repeaters are required to perform entanglement swapping and entanglement distillation [2]. Here quantum memories find their place in the core of quantum repeaters to perform storage and synchronization not only in the repeater but between different nodes of the network.
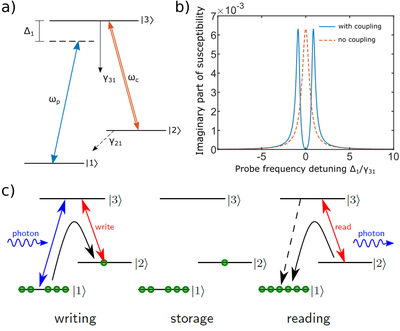
We use warm alkali vapors as quantum memories due to the easy production and handling of vapor cells, fulfilling the requirement of scalability. Using Electromagnetically Induced Transparency (EIT) created by optically addressing the hyperfine transitions in the Cesium D1 line (~894 nm) we create a transparency window in the otherwise absorptive gas [3], see Fig. 1 a) and b). We aim to store single photons generated by Quantum Dots and Spontaneous Parametric Down Conversion sources at 894 nm. This is possible by switching the coupling in the EIT while the photons are traveling through the gas. The traveling photon is absorbed and the information stored as a spin wave in the long-lived ground states of Cs, as shown in Fig. 1 c). Shining the coupling field releases the stored photon after a desired storage time within the limits of the decoherence rate between the ground states.
Figure 1: a) Lambda scheme for EIT. Probe beam is set to the transition |1> - |3>, coupling beam to transition |2> - |3>. b) Imaginary part of susceptibility, related to the absorption of the medium. Splitting of the absorption is observed at resonance when the coupling is present. c) Storage scheme using EIT. A photon is sent through the vapor and the coupling switched off. The photon is absorbed and stored as a spin wave between ground states |1> and |2>. After waiting a certain storage time, the coupling is reactivated leading to the emission of stored photon.
[1] H.J. Kimble; "The quantum internet", Nature, vol. 453, no. 7198, pp. 1023-1030, Jun. 2008, doi:10.1038/nature07127
[2] S. Bratzik, S. Abruzzo, H. Kampermann and D. Bruß; "Quantum repeaters and quantum key distribution: The impact of entanglement distillation on the secret key rate", Phy. Rev. A, vol. 87, no. 6, p. 062335, Jun. 2013, doi:10.1103/PhysRevA.87.062335
[3] M. Fleischhauer, A. Imamoglu and J.P. Marangos; "Electromagnetically induced transparency: Optics in coherent media", Rev. Mod. Phys., vol. 77, no. 2, pp. 633-673, Jul. 2005,
doi:10.1103/RevModPhys.77.633
Contact: Esteban Gomez Lopez
3. Photonic Structures to Enhance Light-Matter Interaction
Here we study the enhancement light and matter interaction by confining light fields in photonic structures placed in atomic vapor environments.
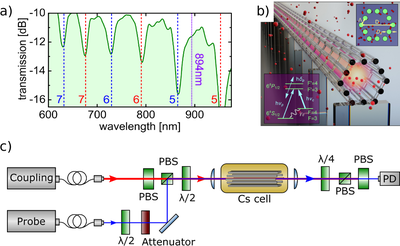
One of the structures of interest is a hollow-core light cage printed in a photoresistive polymer, see Fig. 1 a). Employing 3D printing techniques makes the construction of these structures easy enough for large scale production. The light cage works as an anti-resonant reflecting optical waveguide, which guiding properties can be tuned by changing the geometrical properties of the light cage, like the diameter of the rods and their distancing [1]. The light cages can be coated to protect them from harsh environments like alkali vapors [2]. This allows to create a light cage with high transmission at the Cs D1 line, Fig. 1 b), capable of last long times in the vapor.
By placing the light cage in a vapor cell, we build a platform to perform experiments where the tight confinement of light over long distances has a strong effect, such as Electromagnetically Induced Transparency (EIT) (typical setup shown in figure 1c). The light cage extends the effective interaction length to the whole length of the waveguide resulting in wider transparency windows from EIT which can be used for storage of broadband light pulses.
Figure 1: a) Transmission of the light cage as a function of the wavelenght. A transmission window was tailored to match the Cs D1 line at 894nm. b) Render of the light cage in Cs vapor environment. The EIT is created by probing the transition F=3-F'=3 while coupling the transition F=4-F'=3 of the CS D1 line. c) Experimental setup to perform EIT in a light cage. The light cage is placed inside a glass cell with Cs vapor. Coupling and probe beam are coupled into the waveguide with cross polarization allowing to filter out the coupling beam with an additional polarizer.
[1] C. Jain et al.; "Hollow Core Light Cage: Trapping Light Behind Bars", ACS Photonics, vol. 6, no. 3, pp. 649-658, Mar. 2019, doi:10.1021/acsphotonics.8b01428
[2] B. Jang et al.; "Fine-tuning of the optical properties of hollow-core light cages using dielectric nanofilms", Opt. Lett, vol. 45, no. 1, pp. 196-199, Jan. 2020, doi:10.1364/OL.45.000196
Contact: Esteban Gomez Lopez
4. Narrow-Band Single Photon Source
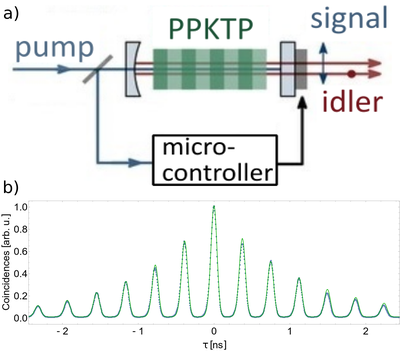
Many applications in quantum optics require the generation of single photons with well-defined frequency and bandwidth. We are using an optical parametric oscillator (Fig. 1) pumped far below the threshold as an ideal tool to tune the frequency and bandwidth of photons generated by spontaneous parametric down-conversion [1-3].
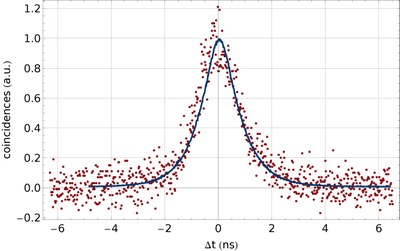
Figure 1: a) Setup of the optical parametric oscillator [3]. Signal and idler photons are generated by spontaneous parametric down-conversion in a periodically poled KTP crystal (PPKTP) which is placed inside an optical resonator. b) Temporal correlation of the signal and idler photons. The measured data (dots) and the theoretical curve (line) show a comb-like structure, which is caused by the cavity. The photons can leave the cavity only after a full round-trip, leading to time difference with vanishing coincidence probability [4]. Therefore, the spacing between the peaks corresponds to cavity round-trip time.
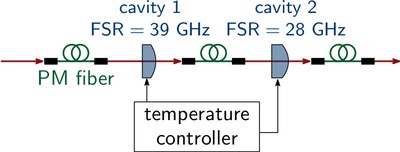
To obtain only photons with the desired frequency, spectral filtering of the generated photons is required. Therefore we developed a fiber-coupled two-stage filter system (Fig. 2) based on monolithic Fabry-Perot cavities [5]. These are extremely stable, polarization independent and can conveniently be tuned by changing the substrate temperature.
Figure 2: Filter system based on monolithic Fabry-Perot cavities with high transmission. By combining two resonators with a different free spectral ranges a band-pass filter with an effective free spectral range of more than 400 GHz and a line-width of about 200 MHz can be realized.
[1] M. Scholz, L. Koch, and O. Benson, Phys. Rev. Lett. 102, 063603 (2009).
[2] M. Wahl, T. Röhlicke, H.-J. Rahn, R. Erdmann, G. Kell, A. Ahlrichs, M. Kernbach, A.W. Schell, and O. Benson, Review of Scientific Instruments 84, 043102 (2013).
[3] A. Ahlrichs and O. Benson Appl. Phys. Lett. 108, 021111 (2016)
[4] C. Müller, A. Ahlrichs and O. Benson Phys. Rev. A 102, 053504 (2020)
[5] A. Ahlrichs, C. Berkemeier, B. Sprenger, and O. Benson, Applied Physics Letters 103, 241110 (2013).
Contact: Esteban Gomez Lopez
5. Conversion of Single Photons
To combine the advantages of entirely different quantum systems – such as quantum dots, atoms and photon pair sources – it can be important to make them interact by the exchange of photons. Furthermore, long distance quantum communication works most efficiently in the telecommunications wavelength range of about 1550 nm.
Inter-conversion of wavelengths can bridge these gaps. We use a nonlinear crystal to perform Difference Frequency Generation in a periodically-poled lithium niobate waveguide. This technique has been shown to be very efficient at converting single photons from the near-infrared to the telecom range, while preserving the quantum properties [1,2].
The nitrogen-vacancy (NV) center is a promising candidate to realize a quantum memory, which is crucial for quantum communication. The NV center emits single photons is in the visible, where an ordinary frequency conversation generates noise at the desired telecom wavelength, reducing the utility drastically [3]. Therefore, we perform experiments to investigate efficient and low-noise conversion of single NV center photons.
[1] S. Zaske et al., Phys. Rev. Lett. 109, 147404 (2012)
[2] Kroh et al. Quantum Sci. Technol. 2 034007 (2017)
[3] J.S. Pelc et al., Opt. Lett. 35, 2804-2806 (2010)
6. Quantum Key Distribution
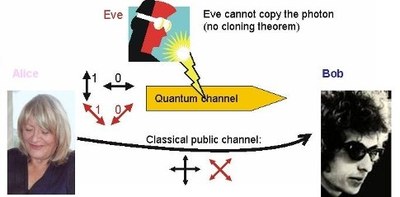
In QKD, two parties, usually called Alice and Bob, want to communicate in a secured way. To do this, they both have to possess a key, which is used by Alice to encrypt a message and by Bob to decrypt it afterwards. To exchange their key, they can use quantum systems, e.g. single photons and exploit the rules of quantum mechanics to ensure secure communication, explicitly the two following rules: a quantum system cannot be measured without perturbing it and a quantum system cannot be copied with arbitrarily high accuracy. A potential eavesdropper (generally called Eve) who tries to pick up the bit sent to Bob will inevitably introduce errors while measuring the system, thus can be detected. If such errors reveal the presence of Eve, Alice and Bob will reject the key and restart communication until a secure key is transmitted (figure 1).
Figure 1: Principle of quantum cryptography in the BB84 protocol with polarization encoding
Today, quantum key distribution (QKD) is the only safe way to communicate secretly, secured by the laws of quantum physics. On the one hand it is already a mature field of research, on the other hand, there is still need for improvement when it comes to transmission rates and distances. Because it is an important application in the field of quantum technology, it is interesting to investigate new light sources and protocols for QKD.
We have used defect centres as single photon sources for a BB84 QKD experiment and evaluated their utility in comparison with other light sources [1]. For this experiment, a post-processing algorithm based on CASCADE was developed (https://github.com/rriemann/privacy-amplification/releases).
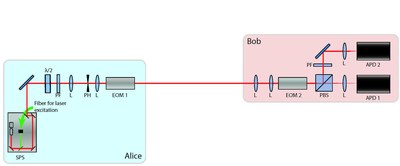
Figure 2: The setup of our QKD experiment. A single photon source (SPS) in the form of a confocal setup which is able to host different defect centres emits photons which are modulated in polarization with an electro optic modulator (EOM) on Alice’s side. On Bob’s side the polarization of the photons is measured with a polarizing beam splitter (PBS) and two avalanche photodiodes (APDs). The basis choice on Bob’s side is implemented with an EOM.
As a byproduct of our research, a quantum random number generator (QRNG) was developed and tested in cooperation with PicoQuant (http://www.picoquant.com) [2].
Currently, a new kind of QKD-protocol is under investigation, where the quantum information is encoded in arrival time and frequency of a photon and the security comes from the time-frequency uncertainty relation. This protocol is especially well suited for free space links, thus a 500m testbed is under development at the moment. The project is conducted in cooperation with the Fraunhofer Heinrich Hertz Institute.
[1] M. Leifgen et al., New J. Phys. 16, 023021 (2014)
[2] M. Wahl et al., Appl. Phys. Lett. 98, 171105 (2011)